ウィルコクソンの順位和検定の効果量には、いくつかタイプがありますが、ここではcommon language effect sizeというものをご紹介します。
U統計量/(グループAのサンプル数 * グループBのサンプル数)
の値を計算すると、グループAから取り出した値がグループBから取り出した値を上回る確率になります。
これが0.5(確率五分五分)からどの程度離れているかで、グループ間の差の大きさがどの程度のものなのかを判断できます。
たとえば、ここに飛行機の到着遅れが、平日か週末かによって影響されるのかを検定した結果があります。
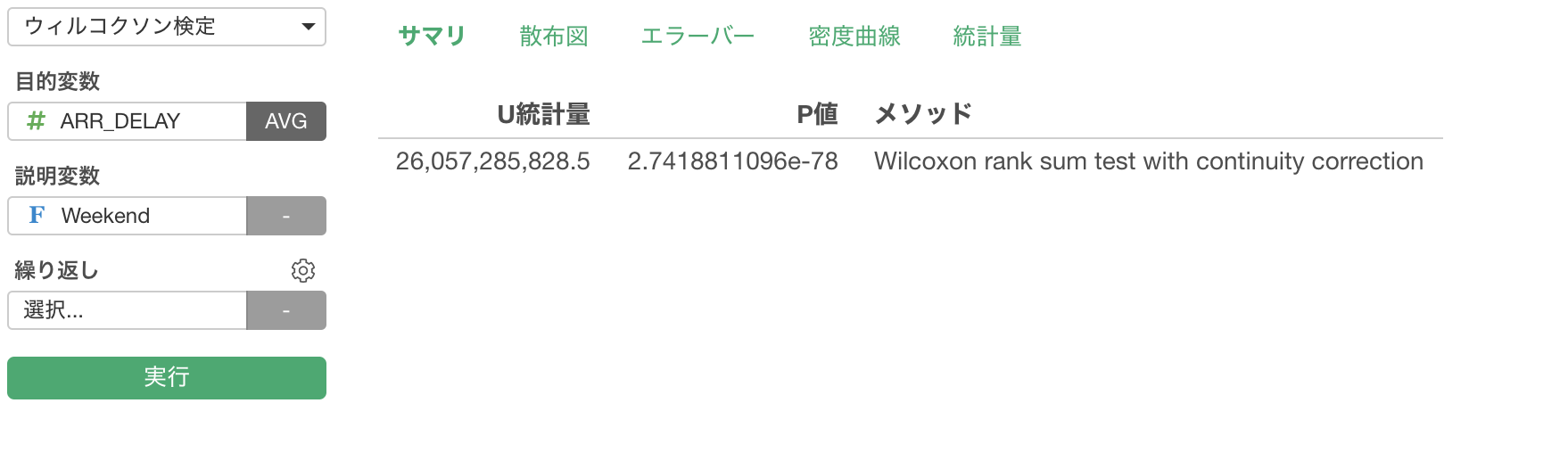
P値は2.74 x 10のマイナス78乗と非常に0にちかく、差が有意であることは確かです。
しかし、この差は気にするに値するような大きさの差なのかを判断するために、効果量としてcommon language effect sizeをみてみましょう。
サマリ・ビューで週末、平日のデータの行数をみます。
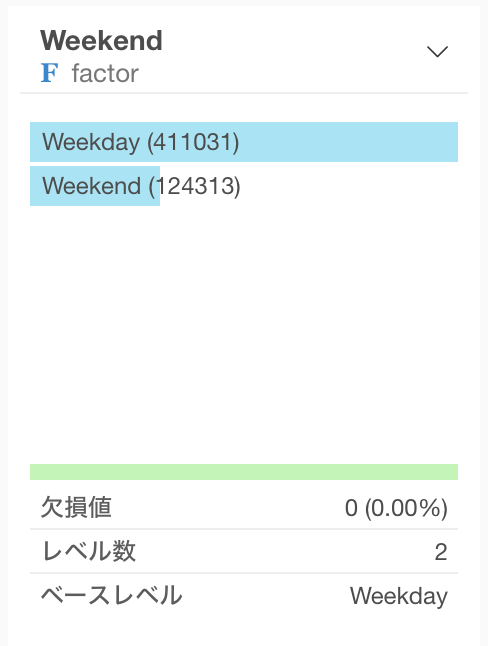
これと、検定結果のU統計量を元にcommon language effect sizeを計算すると、
U統計量/(平日のサンプル数 * 週末のサンプル数) = 26057285828 / (411031 * 124313) = 0.51
となり、平日のフライトと週末のフライトをランダムに持ってくると、51%の確率で平日の側のほうの遅れのほうが大きい、というほどの差ということになります。
この51%対49%という2%の確率の差を、気にするか気にしないかは分析の目的によると思いますが、差の大きさを定量的に捉えたことにより判断がしやすくなったと言えるのではないでしょうか。
