はじめまして。以下どなたかご存知でしたらご教示頂けると幸いです。
複数の外部予測変数を入れて時系列分析モデルを作成するにあたって、
外部予測変数の多重共線性を考慮しないで作成したモデルに比べて、
外部予測変数の多重共線性を考慮して作成した時系列分析モデルの方が精度が低くなる場合、
これはどうして起こるのでしょうか。
多重共線性の強い変数を除外したほうが、モデルの精度が高くなるという認識でおりましたが、
上記のように、そうではないケースがありましたのでお伺いしております。
なお、ここでいう多重共線性の考慮とは、
時系列分析モデルを作成する前に、線形回帰分析でVIF10以上となった変数を外す、
ということを意味しております。
何卒宜しくお願いいたします。
はじめまして。
時系列データの分析のことを詳しく知っているわけではないので、話半分くらいに参考にしていただけますと幸いです。
時系列分析モデルの外部部予測変数を選定する上で、VIFは役に立たないように思えます。
※Exploratoryでサポートされている時系列分析モデルでよく使われるProphetを想定します。
※「モデル構築」からXgboostやRFなどで実行していた場合、すいません。
時系列のデータに対して、線形回帰分析を行うと、線形回帰分析の仮定(特にサンプルの独立性)が守られず、
無関係のデータから意味があるように見えるパラメタの値が得られる、という「見せかけの回帰」問題が起こりやすいかと思います。※ここらへんも処理済であればすいません
その状態で、計算されるVIF値は、変数間の関係を検討する上でそもそも信頼にたらない可能性がありそうです。
VIF値は回帰分析のR2値をもとに計算される指標だと認識しております。
下記は「全く関係のない時系列データxとyの回帰モデルy ~ x」「意図的に時系列データっぽく(詳細は省きます)加工してあるデータxxとyyの回帰モデルyy ~ xx」に対して、シュミレーションし、各回帰モデルのR2値(r.squared)を取り出し、可視化した結果です。
※x1、x2、x3…とyとあってもデータの性質が同じであれば、同じように考えられるかと思います。
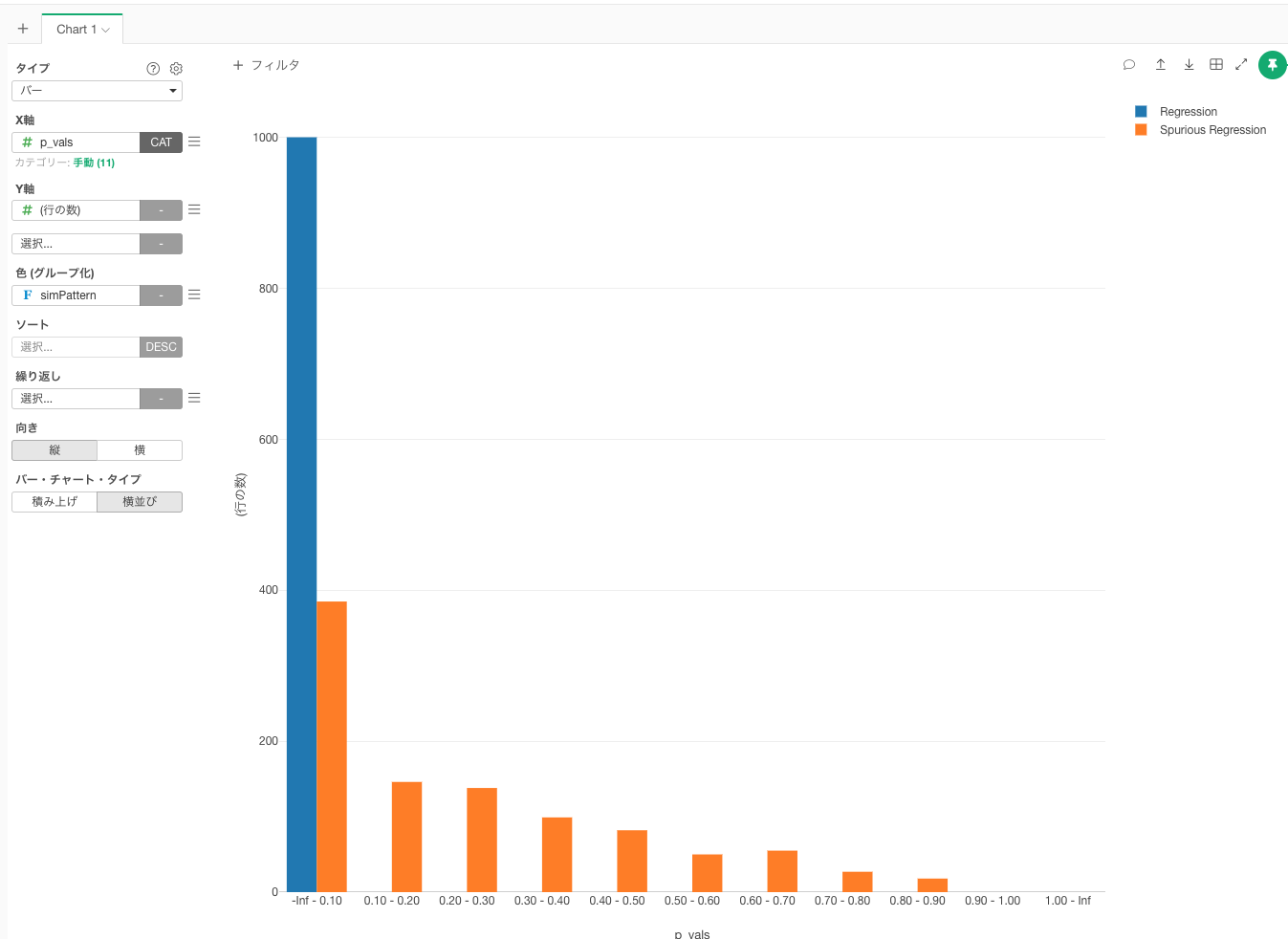
※サンプルサイズ500でデータを生成し、各データで1000回づつ回帰モデルを構築し、R2値を取得して可視化
青色の「全く関係のないデータxとy」では、基本的に0に近いところにある一方で、オレンジ色の「意図的に時系列データっぽく加工してあるデータxxとyy」では、本来関係のないはずなのに、シュミレーションの結果によってはR2値は0.8近くある場合もあります。
値が無意味にばらつくR2使って計算されるVIFをもとに変数選択を行ったとしても、「VIFの値から選定されている変数」と「本当の意味のある変数」がイコールになっておらず、Prophetでは有効な外部予測変数(extra_regressors)として、機能しなかったのかと思います。
Prophetでは、Prophetがどのように外部予測変数をモデルに足し混んでいるかどうか、可視化できたはずなので、その振る舞いをみるのも、考察する上で役立つかもしれません。下記の例では、下がりトレンドに対して、外部予測変数x1、x2、x3は0付近でちょこちょこ動いているだけで有効とは思えません。(そういうデータを作ったので、そうと言われるとそうなんですが。)
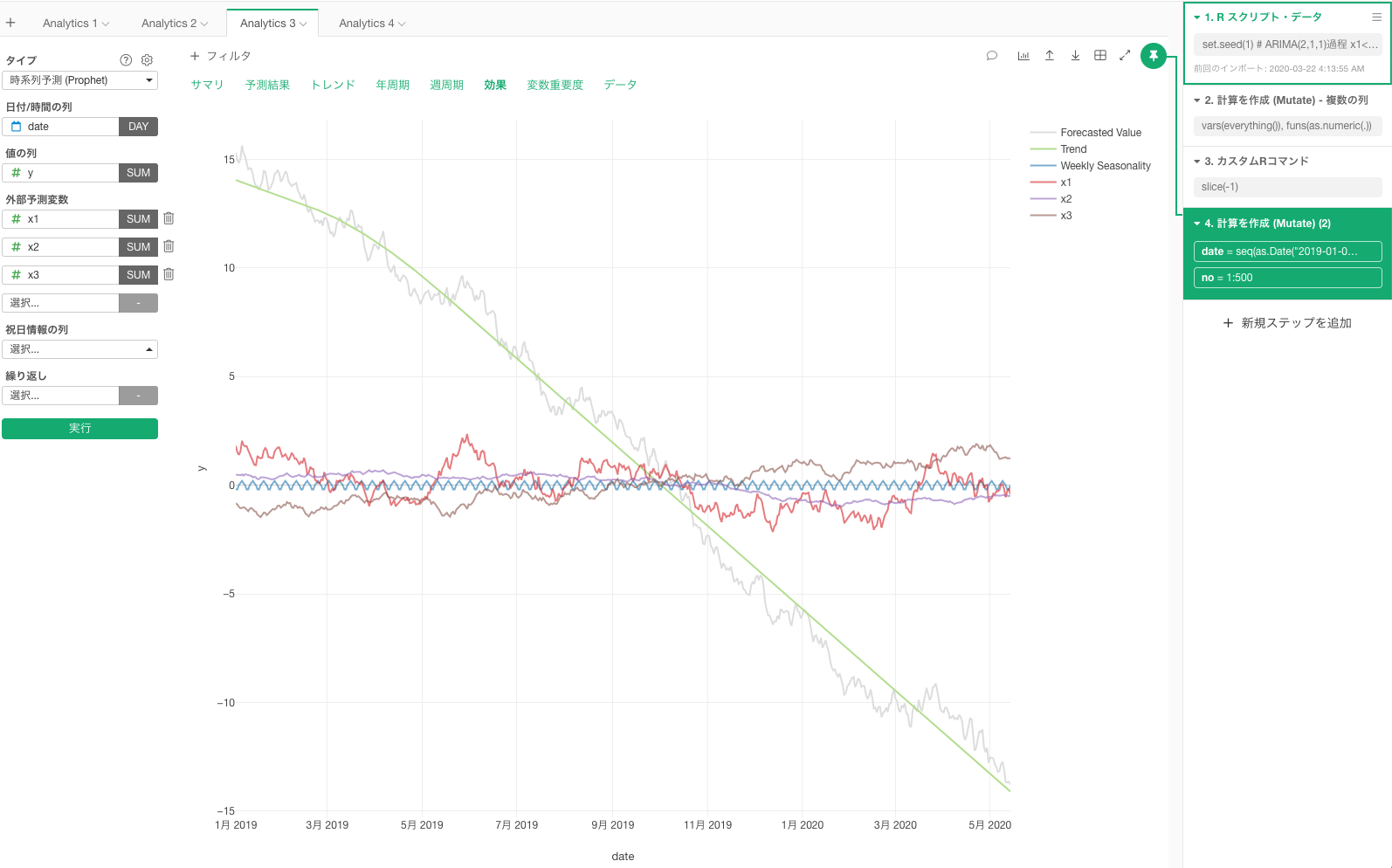
また、別の見方として、回帰分析は「事象説明のために、モデルの係数に興味がある場合」と「予測することに興味がある場合」の2つの使い分けが、分析の目的に応じて発生するかと思います。
前者の場合、マルチコリニアリティを考慮することはモデル解釈の観点から必要になる場合もありますが、後者の予測の場合、マルチコリニアリティがあろうがなかろうが、可能な限り予測値がよくなるように、各パラメタ同士が調整されるので、そもそも多重共線性を考慮されず使用されることも多いように思えます。
このような理由から「多重共線性を考慮なしモデル」よりも「多重共線性を考慮ありモデル」のほうが精度が悪くなったのかと思います。
複数の外部予測変数を入れて時系列分析モデルを作成するにあたって、
外部予測変数の多重共線性を考慮しないで作成したモデルに比べて、
外部予測変数の多重共線性を考慮して作成した時系列分析モデルの方が精度が低くなる場合、
これはどうして起こるのでしょうか。
そのため、今回の場合は、
というようなことが、分析しているデータで起こったのではないでしょうか…かといいつつ、時系列モデルで役に立つ外部変数を効率よく選定するという、これという方法を私も知らないので、やはりドメイン知識を利用しつつ、モデルチューニングを行う必要があるのではないでしょうか。
端切れの悪い回答で申し訳ないですが、ご参考になれば幸いです。
wasabiさん、ご丁寧にご回答頂き誠にありがとうございます。
VIF値の計算のされ方やその可視化の方法など、基本的な部分も含めて認識不足であったので、
今回ご教示頂き大変参考になります。
そもそも時系列モデルはよしなパラメーター調整を行ってくれると理解できましたので、
仰る通り、どの変数を外部予測変数としてピックアップするかが今後のポイントになりそうです。
今回頂いたアドバイスを参考に、有効な手法がないか色々探ってみようと思います。
大変助かりました。ありがとうございます。
ご丁寧にありがとうございます。
となりますとやはり、時系列モデル構築に有効な外部変数の選定にあたっては「見せかけの回帰」が起こらないように処理を工夫してVIFを見るか、手元のデータの特性を考慮しながらチューニングしていくのが良さそうですね。
今後の方針が見え、大変助かりました。どうもありがとうございます。
